第三章  种群生态学

教学目的：通过本章的学习，了解种群的概念、基本特征、结构、分布型、数量动态及生命表的组建及分析，以及生态对策的概念、特点及其在害虫治理中的指导作用。

教学内容：

1. 种群的概念、基本特征；

2. 种群分布类型（经典理论频次计算和聚集指标法的应用）；

3. 种群的生长型和季节消长型（包括种群的生长类型、种群的季节消长类型）；

4. 生命表的组建及其分析；

5. 生态对策的概念、类型与防治策略；

6. 种群数量对策及其调节理论；

7. 种间竞争和种内竞争。

教学重点：种群的概念、特征、分布类型及步骤，生命表的组建及分析以及生态对策的概念；生命表的分析和生态对策的对防治策略的指导作用。

授课方法：讲授、实验

主要参考书目：

《昆虫生态学与害虫预测预报》张国安、赵惠燕主编，2012年，国家十二五规划教材，科学出版社

《昆虫生态及预测预报》第三版，张孝羲主编，2002年，中国农业出版社

《昆虫生态与农业害虫预测预报》牟吉元主编，1997年，中国农业科技出版社

 

第一节  种群的基本特性与种群结构

一、种群的概念、特点及其分类

1、种群（POPULATION）： 是指在一定的生活环境内，占有一定空间的同种个体的总和，是种在自然界存在的基本单位。

2、种群的特点：

a. 种群是通过种内关系组成的一个有机的统一群体，它除具有种的一般生物学属性（形态结构、生活方式、遗传性相同，以及与其它种存在严格的生殖上隔离）外，

b. 还具有群体自身的生物学特性（出生率、死亡率、性比、平均寿命、年龄组成、基因频率、繁殖速率、密度及数量变动、空间分布、迁移率、滞育率）。

c. 种群是一个自动调节系统，具有群体的信息传递、行为适应、数量反馈控制的功能。

3、种群的分类：
a. 同种昆虫由于长期的地理隔离而形成的种群，称为地理种群（地理亚种，地理宗）。
b. 因寄主食物的不同而形成的不同种群，称为食物种群（食物宗、寄主宗）。
c. 有时由于需要研究两种或两种以上的种群，称为混合种群。

二、种群的结构

1、昆虫种群的结构：即昆虫种群的组成，是指种群内某些生物学特性、对环境适应能力或形态上可以是完全相同的个体群在总体中所占的比例。其中主要是性比和年龄组配

性比：是指成虫或蛹雌性与雄性之比。或以雌虫率表示。

年龄组配：是指一个自然种群中各发育阶段（卵、幼虫、蛹、成虫）和同一发育阶段不同发育进度（如各龄幼虫、各级卵、蛹或成虫）的数量比例或所占的百分率

第二节   种群的空间分布类型

一、种群分布型的概念

种群是指在一定空间内同种动物（或植物）有机组合的群体。任何一个动物种群总要占据一定的生殖场所，拥有一定的食物供应范围和活动领域，即生态学中所谓的“空间”。

种群动态是指任何一个种群在一定空间内适应环境的历史。种群动态一方面表现为数量上的增减；另一方面表现为数量上的波动，必然关系到空间的扩张和收缩。因此衡量一个种群昌盛与否，通常采用两个指标，即数量与空间。

由于种群栖息地内生物的（种性、种内和种间关系）和非生物的（气候、地形、土质等）相互作用的关系，就造成了种群在一定空间内个体扩散分布的一定形式，这种形式就称为种群的空间格局或空间分布型。
二、种群空间分布型的类型

（一）分类依据

种群空间格局的变化不仅随着不同的物种而有差异，而且亦随着同一物种的不同世代，同一世代的不同发育阶段，以及同一发育阶段的不同龄期、不同密度而不同。若物种个体间呈现相互吸引，为聚集分布（aggregated  distribution）；若个体间相互独立，则为随机分布（random  distribution）；若个体间相互排斥，则为均匀分布（uniform distribution）。

(二)分类类型

根据种群内个体的聚集程度和方式不同，可把昆虫种群的空间格局分为随机型、均匀型和聚集型三大类。在随机型中包括泊松分布，均匀分布中包括正二项分布，在聚集分布型中包括核心分布(奈曼分布)和负二项分布（嵌纹分布）。
    1、随机型          泊松分布
    2、均匀型          正二项分布

3、聚集型              

嵌纹分布（负二项分布）               核心分布（奈曼分布）

三、种群个体的离散频次分布方法

1、随机型

种群内个体独立地、随机地分配到可利用的单位（生物资源）中去，每个个体占据空间任意一点的概率是相等的，即种群内的个体，相互之间是独立的，一个个体的存在位置不影响其它个体存在的位置。

正二项分布（binomial  distribution）又叫二项分布、均匀分布或一致格局。所谓正二项分布就是指数为正的二项式展开后所得到的各项分布。

正二项分布的特点是：

1、种群内的个体在空间的散布是均匀的；

2、种群内的个体在空间的分布比较稀疏，不聚集；

3、个体间相互独立，无影响；

4、当调查单位内实查的数值比较大时（即密度大时）可成一个对称的或近似对称的次数分布曲线。

一个单位中包含有R个个体的概率为：

          Pr=CnrPrqn-r      (r=0,1,2,3,…,n)

式中：p=   /n,为个体出现的概率；q=1-p为个体不出现的概率；n为组数-1或样方内最大虫数；r为计算项的项数。各项展开的理论频次：

 

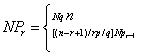
NP0=Nqn

NP1=n/1p/qNp0

NP2=(n-1)/2p/qNp1

NP3=(n-2)/3p/qNp2

NP4=(n-3)/4p/qNp3

2、均匀型

泊松分布 (poisson distribution)

该分布的特点是：      

（1）种群内个体在空间的分布是比较稀疏的；

（2）种群内个体间是相互独立的，即任一个体在某一抽样单位中出现与否与其它个体是否在该抽样单位中存在无关；

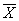（3）其S2/   =1~1.5；

（4）当调查单位内实查数值较小时（虫口密度较小时），可得到一条向右倾斜的偏态次数分布曲线，但当调查单位内实查数值增大时，一般指x≥16时，可趋于正二项分布。

理论通式：  NPr=N(e-mmr/r!)

式中：r为各抽样单位内昆虫数（一般从0，1，2，3，      x）；m为总体平均值，一般用样本平均值     来表示；N为样点总数（样本数），所有频次的和；e为自然对数之底（2.718）.
根据：NPr/NP(r-1)=Ne-m×(mr/r!)/Ne-m×[m(r-1)/(r-1)!]=m/r
         移项得：NPr=NP(r-1)×m/r
计算时往往用简化的递推公式各项展开依次为：
             

 

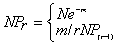
NP0=Ne-m
              NP1=m/1NP0
              NP2=m/2NP1
              NP3=m/3NP2
              NP4=m/4NP3

3、聚集型

聚集分布是指昆虫个体，因种种原因造成的分布不随机性，这种不随机性的显著特点是疏密不匀。也分两种类型：嵌纹分布、核心分布。

① 嵌纹分布（Mosaic  distribution）或负二项分布（Negative  binomial  distribution）   这是昆虫最广泛的一种分布。

该种分布的特点是：

a. 由于种群内个体间具有明显的聚集现象或由于环境条件的不均匀性，使种群个体呈现为疏密相嵌，很不均匀的分布。如麦蚜、棉蚜等；

b.种群内各个体在抽样单位中出现的机会不相等；

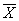c.S2/ 通常介于1.5~3.0之间；

d.种群内个体群之间为Poisson分布，而个体群内个体的分布为对数分布。
    表达式：N（Q-P）-k
    概率通式：NPr=N[(K+r-1)!/r!(k-1)!]Q-k-rPr   
    式中：N为样本总数；r为频次表中的项数，即样方中昆虫数从小到大所排成的项数；

由： NPr/NP(r-1)=N[(K+R-1)!/r!(k-1)!]Q-k-rPr/N[(K+(r-1)-1)!/(r-1)!(k-1)!]

Q-k-(r-1)P(r-1)=(k+r-1)/rP/Q
       移项得：NPr= (k+r-1)/rP/QNP(r-1)

逐项递推公式为：    

 

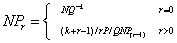
各项展开： NP0=NQ-k
               NP1=(K+1-1)/1P/QNP0=KP/QNP0
               NP2=(K+2-1)/2P/QNP1=(K+1)/2P/QNP1
               NP3=(K+3-1)/3P/QNP2=(K+2)/3P/QNP2
               NP4=(K+4-1)/4P/QNP3=(K+3)/4P/QNP3
               NP5=(K+5-1)/5P/QNP4=(K+4)/5P/QNP4

② 核心分布（contagious  distribution）或奈曼分布（Neyman  distribution）

该分布的特点是：

    a.昆虫种群内的个体在栖息地里呈多数小集团，形成很多核心，这些核心大小大致相等；

    b.在每一个抽样单位中，各个体群之间呈泊松分布，而个体群内的个体亦呈泊松分布；

    c.种群内个体彼此间不是相互独立的；

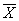d.S2/   =1.5~3.0,  多数昆虫所产卵块孵化为幼虫后,自核心作放射状蔓延,属此种分布。

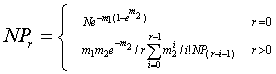概率通式：

 

 

 

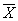
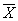式中：m1=      2/(S2-M),  相当于嵌纹分布的K值；

m2=(S2-    )/     相当于嵌纹分布的P值。
令：A=m1*m2*e-m2
各项展开计算公式：
NP0=Ne-m1(1-em2)
NP1=A/1NP0
NP2=A/2[NP1+m2NP0]
NP3=A/3[NP2+ m2NP1+ m22/2!NP0]
NP4=A/4[NP3+ m2 NP2+ m22/2! NP1+ m23/3!NP0]
NP5=A/5[NP4+ m2 NP3+ m22/2! NP2+ m23/3! NP1+ m24/4!NP0]

三、种群空间分布型的测定方法

（一）频次分布测定法

频次分布测定法（determination  method  of  frequency  distribution）是一种经典的方法。基本原理是将实查的种群空间分布信息（如均数、方差和取样数），首先整理调查的原始数据，编制实查频次表，然后计算相应的参数，进而依各理论分布公式算出理论频次分布，最后用实际调查整理的频次与对应的所计算理论频次值进行卡方检验，根据其吻合程度来判断该资料属那种分布型，吻合程度是通过查表与卡方值相比而得出的。

频次分布测定的具体步骤如下：

1、确定调查对象。

2、选好调查标准地。根据害虫发生的情况和危害程度，选择具有代表性的试验地。

3、确定调查方法。包括抽样方案的制定、抽样单位的选择和理论抽样数的确定。

4、整理调查结果。列出每个样方的虫口数（X），和实测频次（f）所组成的频次分布统计表，以求出样本方差（S2）和平均数（x）

5、按照各分布型的概率通式，计算各项理论概率及其相应的理论次数。

进行卡方检验，测定其实测频次与理论频次之间的差异是否显著。

计算卡方值的公式为：

 

然后根据自由度（f）和概率水平（P）查x2值。为了查表方便，这里提早说明各种空间格局类型条件下的自由度：正二项分布和泊松分布为（n-2）,负二项分布和奈曼分布均为（n-3）。在相应和自由度下凡算得卡方累计值大于该自由度下P0.05时的卡方值，则其P〈0.05。表示理论分布与实际分布相符合，也就是不属于该分布。反之，当算的卡方值的P〉0.05时，即表示二者相符合，可以判断为属于该种分布型。

（二）聚集指标法

聚集指标法（Indies of aggregation）的特点：计算简便，可根据其指标的大小来判断种群的分布类型，并对种群个体的行为，种群扩散的序列变化也能提供一定的信息。但其缺陷是判断分布型比较粗放，只分大类，不及经典频次法具体。具体包括：  扩散系数（C ）、    负二项分布K值法、扩散型指数（Iδ）、平均拥挤度、平均拥挤度（X*）与平均数的回归关系法、Taylor幂法

1、扩散系数（C）

所谓扩散系数就是利用均数和方差是否相等的这一特性，进一步求其S2/    的比值，用来估计所检验的昆虫种群是否偏离随机型的一个系数，常记为C，其公式为：

          C=∑(xi-   )2/(n-1)= S2/

式中：xi为每个样本内的虫口数；

为虫口平均密度；S2为方差；n为抽样数。

简单判别：C=1时，为泊松分布；

          C>1时，为聚集分布；

          C<1时，为均匀分布。

2、负二项分x布K值法

负二项分布中的K值的生物学意义是，K值可以作为种群聚集程度的一个度量：K值的大小，反映聚集度的大小，K值愈大，聚集度愈小，K值愈小，聚集度愈大。如K值趋于无穷大时（一般为8以上时），则逼近poisson分布。

注意：用K值法时，由于K值受抽样单位大小的影响，一般最好在同样大小的抽样样方下进行。

用Ca，即1/K来表示，比较方便。

            当Ca=0时，为随机分布；

            当Ca>0时，为聚集分布；

当Ca<0时。为正二项分布。K=x2/(s2-x)

3、扩散型指数（Iδ）

扩散型指数（Iδ）最大优点是分布型、抽样数、抽样单位大小独立。
扩散型指数（Iδ）公式：

 

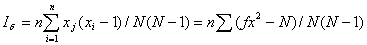
式中：n为抽样数；N为总虫数；xi为第i个样本中的虫口数。

       Iδ=1  为 poisson分布 ；

       Iδ>1为聚集分布；

       Iδ <1 均匀分布。

4、平均拥挤度

平均拥挤度是指平均在一个样方内每个个体的拥挤程度，强调的是个体的平均，而不是象x平方那样是样方的平均。

特点：在种群密度较低时，“0”样方很多，虽然平均数X很小，但实际上在集团中的个体间仍极拥挤，种内竞争激烈，因此平均数X很难反应生物因素的相互影响效应，而x﹡可比较真实的反应出种内竞争等生物因素的作用，在生态学中具有很重要的意义。
    计算公式为：

 

 

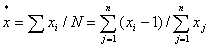
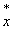
或：    =     +（    /K）  式中K为负二项分布的K值。(大量抽样)

Lwan(1971)提出，用平均拥挤度（    ）与平均数（    ）之比值，作为判断种群空间格局的指标。

当X*/     =1时，为POISSON分布       当X*/      <1时，为均匀分布

当X*/     >1时，为聚集分布

5、平均拥挤度（X*）与平均数的回归关系法

Lwao提出用    与    之间的直线回归关系式中的两个回归系数α，β作为判断种群空间分布型的指标。

    X*=α+β             α   β分别为截距和斜率。

α说明分布的基本成份， β说明基本成分的空间分布型。

     α>0时，个体间相互吸引，分布的基本成分的个体群。

     α=0时，分布的基本成分是单个个体。

     α<0时，个体间相互排斥。

     Β=1随机分布，Β>1聚集分布， Β<1均匀分布

而α与β的不同组合，亦提供种群的不同分布类型的信息。

        当α=0，β=1时，种群分布型为随机。            

（1）α.>0，β=1时，  核心分布、泊松分布-正二项分布

（2）α=0，β>1时，   均为聚集分布       负二项分布

（3）α>0，β>1时     负二项分布

6、Taylor幂法

Taylor指出：在自然种群中，多属不随机分布，样本均值（x）与方差（S2）之间是不独立的，方差常随均值的增加而增加。他从大量的生物学资料中，得出方差的对数值与均数的对数值存在着下列回归关系：

 

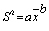
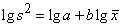
截距a是一个取样统计因素

斜率b是表示当平均密度增加时，方差的增长率，因而它是聚集度对密度依赖性的一个尺度。

最后利用参数a、b的取值，可对种群个体数散布的随机或非随机状况作出判断。方法如下：

对数转换为：

利用参数的取值，可对种群个体散布的随机或非随机状况作出判断。

判断法则如下：

（1）若loga=0，(即a=1)，且b=1，则为随机分布；

（2）若loga>0，(即a>1)，且b=1，则种群在一切密度下        都是聚集的,但其聚集强度不因种群的改变而变化；

（3）若loga>0，(即a>1)，且b>1，则种群在一切密度下都有是聚集的，聚集强度随种群密度的升高而增加；

（4）若loga<0，(即0<a<1)，且b<1，则种群密度越高，分布越均匀。

第三节  昆虫种群的数量变动

一、数量变动的参数

昆虫种群数量的变动主要取决于种群基数、繁殖速率、死亡率、和迁移率等。

1、种群基数（N）是指前一代或前一时期某一发育阶段（卵、幼虫、蛹、成虫）在一定空间的平均数量。是估测其下一代或后一时期种群数量变动的基础数据。在调查N的过程中，应注意取样调查的准确性和代表性。

对一些扩散能力强或具有迁飞性的昆虫的成虫，常以1支黑光灯诱集的上代总数量作为下代的种群基数。

也可在一定空间内，标记（如用喷涂颜料、示踪原子等方法）释放和捕回成虫。按释放或捕回的数量比来估计种群基数。

种群基数=（捕回成虫总量/捕回标记成虫量）*释放标记成虫量。

2、繁殖速率（R）

是指一种昆虫种群在单位时间内增长的个体数量的最高理论倍数。它反映了种群个体数量增加的能力。

繁殖率的大小取决于种群的生殖力、性比和一年发生代数。可以用下式表示：
                           R=（e*f/(m+f)）N
    其中e为单雌平均生殖力(产卵量)，m为雄虫数，f为雌虫数，N为一年发生代数。 
    3、死亡率和存活率

种群的死亡率（d）是指在一定环境条件下和一定时间内的生态死亡率 ，它是因时间、环境条件而变化的。一般用在一定时间内种群死亡个体数占总数的百分率表示。存活率s=1-d

4、迁移率   迁移率（M）是指种群在一定时间内迁出个体和迁入个体数量差占总体的百分率。一般情况下，种群无明显的扩散和迁移，其迁移率可视为零。    

 综上所述，昆虫种群的数量变动的基本模式可以概括为：

     

 

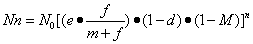
 或  Nn=N0〔R×(1-d)×(1-M)〕n

5、昆虫的种群数量变动也可用种群消长指数

（In）表示。消长指数是指种群至第n代（或第n个发育阶段）时的数量与种群起始数量之比。
即：    In=Nn/N0=〔e×f/(f+m)×(1-d)×(1-M)〕n
    如I=1，表示该种群经N代后，数量未变；

    若I＞1或I＜1，则表示该种群经几代后，其数量增加或下降。
       由于昆虫各代的生殖力、性比、死亡率等不同，同一世代的各个发育阶段（卵、各龄幼虫、蛹、成虫）的死亡率等也不相同，这样有时需要计算综合消长指数（I），即：

     I=I1×I2×I3……In
     I=N1/N0*N2/N1*N3/N2……Nn/Nn-1

二、种群的生长型和季节消长类型

（一）种群的生长型

种群的生长型（Population  growth  form）又称为“种群在时间上的分布”它是在一定条件下，单种种群在时间序列上数量增减的变化形式。

在实验条件下，它主要有两种类型：

J型生长型，即种群数量开始时增加迅速，后因环境因素抑制，数量突然下降。

S型生长型，即种群数量开始时增加缓慢，随即迅速增加，几呈直线上升，然后又增加缓慢,最终达饱和状态，种群数量不再增加。

但这两种生长型也常因物种和环境而发生改变或联合。

（二）种群数量的季节消长类型

昆虫的种群数量是随季节的变化而消长波动的，这种波动在一定空间内常有相对的稳定性，因而形成了昆虫种群的季节消长类型。现将一些重要的农业害虫种群数量的季节消长归纳为以3个类型

1、单峰型  单峰型是指一年内昆虫种群数量只出现一次高峰。又可分为前峰型和中峰型两类：前者是在生长季节前出现种群数量高峰。后者是在生长季节中期出现高峰。

2、双峰型  双峰型是在生长季节前、后期（春、秋）各出现一次高峰，故又称为马鞍型。

3、 多峰型  多峰型是指昆虫种群逐季递增。出现多次峰期，故又称为阶梯上升型或波浪型。

第四节  昆虫种群生命表

一、    生命表的概念、特点、应用

1、生命表的概念

生命表（life table）是指将一定种群的死亡数量、死亡原因、死亡年龄（时间）等资料列成表，以便分析该种昆虫种群生活史过程中引起数量变动的原因，是研究昆虫数量动态的重要方法之一。

2、生命表的特点

① 系统性：表现在它系统地记录了自然条件下和实验条件下昆虫种群在整个世代从开始至结尾的生存或生殖的情况。
    ② 阶段性：表现在它分阶段地记录了各虫态，各年龄或各年龄组的生存和生殖情况。
    ③ 综合性：表现在它记录了影响种群数量消长的各种生物和非生物因素的作用形式。
    ④ 关键性：表现在通过对关键因子的分析，找出在错综复杂的综合因素中的关键因子和关键虫期。

3、生命表的应用

① 应用于害虫的数量测报（由描述性的定性的到解释性的定量化的转变）。
② 应用于评价各种防治措施对控制害虫数量的作用。除了能精确分析出单项措施在某个特定时刻的防治效果外，还能从整个种群数量变动的估值来评价防治措施的最终效果。
③ 应用于害虫的科学管理上。
④ 应用于种群数量变动和模式化表达。即模型的建立。

二、生命表的类型及基本形式

生命表有特定时间生命表（time-specific  life  table）和特定的年龄生命表（age- specific  life  table）两种类型，分别适用于世代重叠和世代较离散的昆虫。

特定时间生命表特定时间生命表是指在昆虫种群是静止（后一时间的种群与前一时间的种群的比基本上为1），而世代重叠、年龄组配稳定的前提下，在特定的时间单位内（如月、旬、周、日等）的一种生命表。

它可获得在特定时间内种群的存活率和出生率，适用于世代和年龄组配重叠的昆虫，可估算出种群在各时间内的死亡率、平均生命期望值和世代平均时间，但不能分析死亡原因和关键因素。

1、存活生命表

在特定时间内对种群随机抽样，检查各期的个体数，其个体数差即死亡数，推算各期的死亡率和平均生命期望值。如下表即为假设的存活生命表

下面是所建生命表中各项含义：

x为按年龄或一定时间划分的单位时间期限（如日、周）；

Lx为第x天存活的数量；

dx为第x天死亡数量，即lx-Lx+1；

1000qx为第x天时间内死亡率×1000，即为（dx/Lx）×1000；

Lx为相当于时间第x到第x+1时的生存个体平均数，即为（Lx +Lx+1）/2；

Tx为Lx、栏从底层向上累加的共计数，即Tx=Lx+Lx+1，即剩余总寿命；

ex为平均生命期望值（x时间后的个体平均寿命），ex=Tx/Lx，如ex为该虫x1时间的理论平均寿命。

 

表2.1  假设某虫的存活生命表

x	lx	dx	1000qx	Lx	Tx	ex
1	1000	300	300	850	2180	2.18
2	700	200	286	600	1330	1.90
3	500	200	400	400	730	1.46
4	300	200	667	200	330	1.10
5	100	50	500	75	130	1.30
6	50	30	600	35	55	1.10
7	20	10	500	15	20	1.00
8	10	10	1000	5	5	0.50

下面是横列中各项的计算推导方法：
    生命表中只有lx和dx是实际观测值，其他各式各栏都是统计数值。
    Lx+1=lx-dx    如14=13-d3=500-200=300
    Lx=(lx+lx+1)/2  or(Lx=lx-1/2dx)    L2=700-200/2=600
    Tx=  Lx=Lx+Lx+1+Lx+2      T3=L3+L4+L5+L6+L7+L8=400+200+75+35+15+5=730
    Ex=Tx/lx    e1=2180/1000=2.18       e4=330/300=1.1
    1000qx=dx/lx*1000        1000q1=300/1000*1000=300

2、特定年龄生命表

特定年龄生命表是以种群年龄作为划分时间的标准，系统观察并记载不同发育阶段或年龄区组中的死亡数量，死亡原因以及成虫阶段的繁殖数量。

 

 

表2.3  一个理想种群生命表（仿WOODS）

年龄（虫期）	存活数lx	死亡原因dxF	死亡数dx	死亡率100qx(%)	存活率Sx
卵（N1）	6000	寄生	3000	50	0.5
一龄幼虫	3000	天气	2000	67	0.33
二龄幼虫	1000	寄生 捕食 小计	200 300 500	20 30 50	0.5
蛹	500	寄生或捕食	100	20	0.8
成虫	400	性比 （雌虫占40%）	80	20	0.8
雌蛾×2	320	生育力下降	160	50	0.5
正常雌蛾×2	160	成虫扩散与死亡	140	88	0.12

期望卵量=正常雌蛾数×每雌蛾的最大产卵量=160/2×200=16000

实际卵量（N2）=20/2×200=2000

趋势指数=N2/N1=2000/6000=0.33

qx为100dx/lx

趋势指数：种群数量的增长倍数

下表为吴坤君1977年在江西省观察和组建的第四代棉铃虫在棉田的自然种群生命表

表2.4   第四代棉铃虫自然种群生命表

发育期(X)	每一虫期开始时存活数(Lx)	死亡原因 (dxF)	每一虫期内死亡数(dx)	死亡率(qx)(%)	存活率(sx) (%)
卵期	1000.0	捕食性天敌 寄生性天敌 自然损失(未授精等) 合计	106.5 76.5 74.5 257.5	10.65 7.65 7.45 25.75	74.25
孵代期	742.5	捕食性天敌 胚胎死亡 自然损失 合计	60.1 27.8 352.7 440.6	8.10 3.75 47.50 59.35	40.65
1~3龄幼虫期	301.8	捕食性天敌 寄生性天敌 自然死亡 合计	137.2 6.7 40.3 184.2	45.43 2.23 13.34 61.00	39.00
4~6龄幼虫期	117.7	捕食性天敌 寄生性天敌 合计	39.8 0.2 40.0	33.80 0.20 34.00	66.00
蛹期	77.7	灌溉等	32.6	42.00	58.00
成虫 ♀×2	45.1 44.2	性比（♀∶♂=49∶51）	0.9	2.00	98.00
全世代			955.8	95.58	4.20

以预测第五代棉铃虫卵量及其种群增长趋势。

三、种群生命表的分析

1、关键虫期和关键因素的判断

关键虫期和关键因素是指某一虫期和某一因素能极大的影响昆虫整个种群未来数量变化的虫期和因素。

进行关键虫期的分析，至少要有5年或5年以上的同代次的生命表资料，才能进行合理的变量分析。常用的方法有K值图解法和相关回归分析法。

(1) 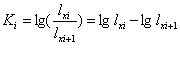 图解法    K值是前、后相邻的两个发育阶段（或因素）的存活虫数（lx）的比值的对数值。即：

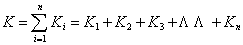全世代各发育阶段的K值之和，称为K（总K值），即：

以年份为横坐标，以K值为纵坐标，绘制总K值和各发育阶段（或各因素）（KI）的坐标图，看那一发育阶段（或因素）的图象与总K值的图象最为相似，则这一发育阶段（或因素）即为关键虫期（或关键因素）。

（2）相关回归分析法

其中又有斜率（b）法和决定系数（r2）法两种。

①     斜率法 以各发育阶段（或各因素）的KI值为自变量（X），全世代总K值为因变量（Y）；或以各发育阶段（或各因素）的存活率（或死亡率）的对数值为自变量（X），以下代虫数（或种群增长指数I）的对数值为因变量（Y），代入下式，分别求得各自的b值，

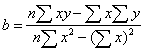
当b>1时，b值最大的发育阶段（或因素）为关系虫期（或关系因素）；当b<1时则反之。

②决定系数法 

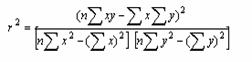同上，将各发育阶段（或因素）的自变量(x)和因变量(y)，代入下式，分别求得各发育阶段（或各因素）的决定系数（r2），即相关系数（r）的平方。其中发育阶段（或因素）的值最大者，即为关键虫期（或关键因素）。

 

 

2、种群控制指数 庞雄飞（1990）提出利用种群的控制指数（index  of  population  control,IPC）来分析种群数量动态。控制指数是指以被因素作用的种群趋势指数（I′）与原有种群趋势指数（I）的比值，即IPC= I′/I，故IPC值是引起种群趋势指数改变的倍数。趋势指数即增长指数，I=N1/N0。

控制指数是分析控制因素对种群系统控制作用的一个指标。如作用因素I的控制指数为：IPC=I=1/Si；如作用因素为n个，则控制指数为：

种群控制指数的测定，也可用于综合分析天敌、药剂防治等对种群数量发展的影响程度，以评价不同防治措施的效果。

3、种群的存活曲线

⑴ 种群的存活曲线定义：

在某一特定时刻，种群中的同龄个体随时间移动而减少的现象，可以用一条曲线来表示，这条曲线称为存活曲线。如以发育阶段（年龄）为横坐标，存活数（或存活率）为纵坐标，绘成的不同发育阶段的存活数（Lx）曲线。存活曲线是建立预测预报的基础。

⑵ 存活曲线的类型

DEEVEY（1950）比较了各种动物的生命表，指出存活曲线大致分为三种类型

Ⅰ型：这类动物中，绝大多数个体均能实现其平均寿命，待达到其固有的寿命时，几乎同时死亡，就是说，死亡率主要发生在年老的个体。这样Lx曲线呈现明显的上拱形。当存活曲线为该类型时，生命期望ex将随年龄的增加而增加。饥饿的果蝇。如图第一种类型。

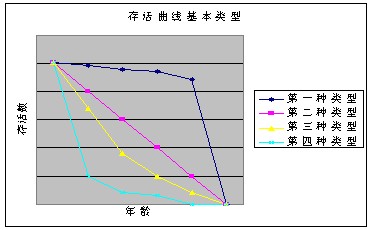Ⅱ型：这类动物在各年龄组均维持同样的死亡率，亦即每个单位时间内或年龄组内死亡数相等，因此Lx曲线呈一直线，也即ex呈常数。例如水螅

算术直线型，如图第二种类型，即每单位时间内的死亡数为常数。
        对数直线型，如图第三种类型，即每单位时间内的死亡率为常数。
     Ⅲ型：这类动物在幼年有极高的死亡率，因此Lx形曲线呈下拱形，这时ex将随年龄增加而减小。如图第四种类型。

存活曲线的意义：了解农业害虫的存活曲线，可明了其易遭伤亡的发育阶段，以分析确定适宜的防治时期。

第五节  昆虫种群的生态对策

一、生态对策

1、生态对策定义------生态对策（bionomic strategy）又称生活史对策（life history  strategy）：即昆虫在进化过程中，经自然选择获得的对不同生境的适应方式。昆虫的生态对策是其对生态环境适应能力的体现。

2、生态对策的类型

昆虫种群的大小和变化速度主要取决于昆虫种群的内禀增长率（r）和环境容量（k）。种群的内禀增长力是指在特定的环境条件下，具有稳定年龄组配的种群的最大瞬间增长速率。环境容量是指在食物、天敌等各种环境因素的制约，种群可能达到最大的稳定的数量。r反映了昆虫种群的增长速率，k反映了昆虫种群发展的最大范围。所以，当k值保持一定时，r值愈大，种群增长速率愈快，种群愈不稳定；当r值保持一定时，k值愈大，种群发展的范围愈大，种群愈趋向稳定。

根据r值和k值的大小，可将昆虫种群基本上分为两个生态对策类型。

（一）K—对策者类型r值较小，k值较大；种群密度比较稳定，经常处于环境容量水平，称为K—选择，属于K选择的生物，称为K类有机体。这类有机体体型常较大，寿命与世代亦较长，繁殖能力小，但常具有完善的保护后代的机制，因此，其后代的死亡率较低，通常不具有较强的扩散能力。

（二）R—对策者类型r值较大，k值相应较小；种群密度比较稳定，很少达到环境容量水平，称为R—对策。属于R选择的生物，称为R类有机体，这类生物有机体的体型往往比较小，寿命以及每个世代的周期较短，繁殖能力很强，但常没有完善的保护后代的机制，因此，其后代的死亡率较高，通常具有较强的扩散迁移能力。

根据K对策和R对策型的特点，可为害虫的防治提供参考。对R类对策的害虫其繁殖力较大，大发生频率高，种群恢复能力强，许多种类扩散迁移能力强，常为暴发性害虫，虽有天敌侵袭，但在其大发生之前控制作用比较小。故对此类害虫防治策略应采取以农业防治为基础，化学防治与生物防治并重的综合防治。单纯的化学防治则由于此类昆虫的繁殖能力强、种群易于在短期内迅速恢复，特别是容易产生抗药性，但在大发生的情况下，化学防治可迅速压低种群数量。同时应研究保护利用和释放相应的天敌昆虫，充分发挥生物防治的控制效应。

中间型：实际上生物的生态对策从K-对策到R-对策是一个连续的系统，称为R-K连续系统。在这个系统中，按照K类选择和R类选择的不同程度排列各种各样的生物，除极端的K 对策型和极端的R对策型外，存有许多过渡的中间型。所以这两种对策型的划分也是相对的。

 

表4.1  R—对策及K—对策的比较表

二、栖境特性和生态对策的关系

栖境：对任何一种动物来说可以定义为整个生活期间活动所到达的地区。

与生态对策有关的栖境特性可以包括以下三个方面。

1.栖境的稳定性  即在一特定地理位置上，特定生境类型所保持的时间长度。其稳定的意义取决于有机体世代的长短（T）与栖境对有机体有利的时间（H）之间的比率（T/H）。这种比值愈小表示栖境稳定。

2.时间上的变异性  在一定地点有机体生存的期限内，随着环境条件在时间过程中的便宜，环境的负荷量（K）也随之而变化（也称为“时间上的异质性”）。K的变化可以是周期性的或是可预测性的，也可以是非周期性的或是随机性的。

3.空间上的变异性即栖境是成片的还是分割成不连续的小块。

上述三方面的特性对于种群生态对策的形成均有影响。但其中稳定性常起决定作用。也就是可以把注意力集中在分析（T/H）比值上。但世代的长短/环境有利（T/H）近似于1时，任何一世代的种群对下一代的资源状况无影响。因此，过度拥挤的种群也不会在进化上留下不良的后果。在这种环境下所生存的物种常是积极的进取者，或称为“r类对策”的有机体。相反，在栖境相对稳定的环境中，也就是（T/H）〈 1 ，此时环境负荷量k虽然相对的较为稳定，但是显著的超负荷现象将使k值有所下降。如果当代的种群密度过大时，便会发生不利于以后世代的后果。同时，在这种稳定的栖境中也将会有许多其它的物种迁入并定居下来，造成各种类型的种间竞争，包括捕食现象将因此而激化。在此环境中生活的物种常有高的取食率而在自然选择中被保存下来。这样的生态对策，就称为是k类对策。

三、昆虫的生态对策和防治策略

根据K对策和R对策型的特点，可为害虫的防  治提供参考。对R类对策的害虫其繁殖力较大，大发生频率高，种群恢复能力强，许多种类扩散迁移能力强，常为暴发性害虫，虽有天敌侵袭，但在其大发生之前控制作用比较小。故对此类害虫防治策略应采取以农业防治为基础，化学防治与生物防治并重的综合防治。单纯的化学防治则由于此类昆虫的繁殖能力强、种群易于在短期内迅速恢复，特别是容易产生抗药性，但在大发生的情况下，化学防治可迅速压低种群数量。同时应研究保护利用和释放相应的天敌昆虫，充分发挥生物防治的控制效应。

对K-对策型害虫：虽然其繁殖力低，种群密度一般较低，但常直接为害农作物和林木的花、果实等造成直接的经济损失。故对其防治策略应为农业防治为基础，重视化学防治防治，采用隐蔽性、局部性施药，坚持连年防治，以持续压低种群的密度。

对一些中间型害虫，利用生物防治往往可以收到良好的效果，而不合理地利用化学防治很可能造成再猖獗。

第六节  种群数量和平衡及其调节理论

影响种群出生率、死亡率和迁移率的各种因素都对种群数量波动起作用。对于昆虫种群波动的重要原因及种群自然调节机制，各学者的观点不同，重要有以下5个学派。

1.生物因素学派  认为昆虫种群是一个自我管理系统，能按自身的性质和环境状况调节其密度，使种群密度在环境中呈平衡状态，捕食、寄生和种间、种内对共同资源的竞争。即不能决定种群密度的平衡。代表人物（Howard（1911）、Fiske（1911）、Nicholson（1933））。

2.气候因素学派  认为昆虫种群密度的波动主要是当地的气候条件对种群的发育速率和存活率的影响。尤其是对昆虫幼期种群密度影响比较大，所以气候因素是决定因素，而生物因素则影响不大。该学派反对将环境因素分为密度制约因素和非密度制约因素及平衡密度等概念。代表人物（Bodenheimer，1928）

3.综合因素学派  认为单纯从生物因素或气候因素来分析昆虫种群数量的波动是片面的，因为他们在不同条件下，不同昆虫种间所起的作用不同。代表Milne（1957）、Buktpob（1955）。

4.动态平衡学派  认为昆虫种群数量能维持在一定水平，是由于种群与生境之间建立了一种动态平衡关系，动态平衡是种群在长期波动中的表现三个过程：代表（Richards（1968）、Clarks（ 1954 ））调节过程，当种群密度达到平衡值以上时，个体数的增加受到抑制，当种群密度在平衡值以下时，则存有促进个体数增加的反馈机制。

变动过程，使种群密度偏离平衡值诸因素的作用过程。主要是由非密度制约因素和逆密度制约因素所引起的过程。

条件过程，规定种群平衡密度上下限或引起种群平衡水平变动的诸因素起作用的过程。

5.自动调节学派  该学派以内源性因素分析说明昆虫种群数量的波动，认为昆虫的行为、生理、遗传影响种群的的出生率、死亡率和迁移率，引起种群数量的波动。

代表：Ford（1931）、Chitty（1955）、Wedwards（1962）

昆虫种群数量波动的原因十分复杂，在不同的时空条件下，环境因素和自我调节的作用过程都不一样，即引起种群数量波动的主导因素也不相同，应因虫、因地、因时、因环境条件进行具体分析。