第八章 数理统计预测法
教学目的:通过本章的学习,学会根据试验的要求选取适当的抽样方法和进行简单的实验设计,实验数据的统计代换,以及利用一元线性回归预测式预测害虫的发生期。
教学内容:预报因子选取的原则和方法、线性回归预测式的建立和应用、常用的抽样方法和单位、常用的统计代换方法
教学重点:预报因子的选取,常用的抽样单位和方法; 线性回归预测式的建立和应用。
授课方法:讲授、实验
主要参考书目:
《昆虫生态学与害虫预测预报》张国安、赵惠燕主编,2012年,国家十二五规划教材,科学出版社
《昆虫生态及预测预报》第三版,张孝羲主编,2002年,中国农业出版社
《昆虫生态与农业害虫预测预报》牟吉元主编,1997年,中国农业科技出版社
数理统计预测法,是利用统计学原理,从害虫发生的历史资料中,概括出环境因子与虫害发生之间的内在联系,建立数学模型,然后根据目前环境因子的情况,来预报未来害虫发生的情况。
数理统计预测预报必须要有多年的田间系统调查资料,将这些资料选择其中有关部分,进行统计分析,得出有关预测预报实用的数学模型,才能加以应用。
数理统计预测法的优点
以前各类预测预报方法,可以称为实验生态、生物学方法,优点:是生态学、生物学、生理学意义较明确.缺点:必须进行田间的系统调查和室内饲养观察,工作量比较大、另外实验法一般只能作中、短期预报,时间较短。
统计预报法,是对多年的历史资料进行统计分析,尔后得出数学模型,就可以不用田间系统调查和室内饲养观察,因而可以大大减少工作量,同时,可作较长时期的预报,并能进一步利用电子计算机作害虫的预报。近二十年来,特别是近十年来,数学方法大量渗入害虫预测预报中,而气象预测预报中的手段也大量引入害虫预测预报中,致使害虫预测预报从方法上,使害虫预报工作向前迈进了一步,为进入电子计算机时代打下了基础。现将预测预报中常用数理统计方法介绍如下。
第一节 预报因子的选取
一、预报因子的选取
预报因子的选取是进行数理测报工作的前提,在准备建立预测模式前,首先要从多年积累的资料中,筛选同预报量有关的因子。
预报量是指预报害虫发生的主要特征,(即在不同的情况下)预报害虫的发生期、发生量、发生范围以及危害程度等。
预报因子简称为因子,影响害虫发生的因素都是预报因子(但不一定都能入选)预报因子有生物的如天敌;非生物的如气温、降雨量、相对温度、光照等。
预报因子和预报量通称为预报的要素。
二、选取预报因子的原则
(1)样本数要足够多。样本数量太少,容易碰到由于样本的随机波动而造成较高的符合率的假象。一般有10-20个就可以了。
(2)选择因子的数目要恰当,因为选择因子太少,则提供信息不足,预报能力差,选择因子过多,计算麻烦且当样本数较少更易引起误差。一般认为选择因子的数目最好不超过样本的1/5-1/10,如10个样本选1-2个因子。
(3)选择准主导因子,并要选好能互相配合,互相弥补的次要因子,与主导因子互相搭配,但注意不要把一些虽然与预报量相关性好,但它们的作用是重复的因子。这样的因子,只是单独对预报量发生作用,并不是同主导因子配合共同起作用,也不能起到弥补的作用,这样的因子不宜作为辅助因子。如某个月的平均气温和平均最高气温以及积温,不宜同时采用。
(4)尽可保留因子中关于预报对象的原始信息,选择因子最好用原始数据建立预测式,如果将预报因子分级(调查时没有量,只有重、中、轻)、编号或转换为(0,1)资料,就会损失信息,但分级、编号、转换、可简化计算,因此,要权衡得失,恰当处理。
(5)选择相关性好而且相关性稳定的因子。用多因子作预报,至少要有一个预报因子与预报量相关性好且相关性稳定。这可以通过相关性检验和多年经验求出。
三、选取预报因子三个注意
1.应有科学的依据
自然界的事物都是有联系的,如害虫的发生规律性和客观环境之间是有联系的,不能把没有科学依据的资料硬往一块凑,例如预测粘虫幼虫的发生量,应从温度、湿度、作物种类,以及天敌等经前人研究已经认可的有关因子出发考虑,而不能把蚜虫的天敌蚜茧蜂作为预报粘虫发生的因子,至少是不能作为主导因子。
2.应有推理的依据,所选因子要经得起推敲,如不少人认为蚜虫的基数与其发生量关系较密切,但仔细分析,蚜虫世代短,繁殖快,天敌控制复杂,到7-8月间受气温影响很大,而基数则是无关紧要的。
应有实验的依据,选因子最好在实验基础上,确认该因子与预报量有关,尔后再作分析。
第二节 线性相关与一元回归式的建立及应用
一、选取预报因子
(一)资料分布图方法
将预报量(Y)作Y轴,将预报因子(X)作X轴,将历年的Y、X数值,描点在坐标上。点子密集在一条狭长的带内,而接近一条直线或一条曲线,说明二者相关性比较密切,可以选作预报因子;如果点子分散,不在一条狭长的带内,表示相关性不强,不宜选作预报因子;如果点子排成圆形,或排成平行于轴的矩形,则表示无线性相关性;点子排列接近一条直线者,称为有“线性相关”;点子排列接近一条曲线者,称为有“非线性相关”,或称有曲线相关。
(二)相关系数法
衡量两变量相关的最好方法是求相关系数,然后查相关系数检验表,检验相关是否达到一定显著水平。如果达到,则可选作预报因子。
二、相关系数的计算
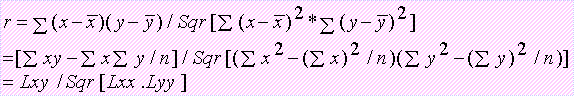
一元线性回归式的建立和应用
回归一词(Regression)原来含义较狭窄,英国高尔登氏(F.Galton)在1889年,在遗传学论文中首先应用此词。他发现儿子的平均成长高度,介于父亲高度和一般种族平均高度之间,父亲矮的其儿子的平均高度较父亲高,比一般低,父亲高的其儿子的平均高度,较父亲低,但比一般平均高度又高,这就是说后代的高度有返回于种族平均高度的趋势,亦即回归一般平均高度,这就是最初在遗传学上“回归”的意义。现在统计上,多表示观察点回归于某一数学模型,比如直线、曲线等。
(一)直线回归
直线回归的一般表达式:Y=a+bx 统计上读作Y依X的直线回归
X为自变量,Y是和X的值相对应的依变数Y的点估计值,理论值。
A是截距,是当X=0时的Y值
B是斜率,也叫回归系数,即X每增加一个单位数时Y平均地增加(b>0)或减少(b<0)的单位数。
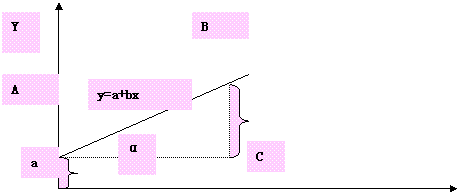
回归式 a、b值的图解求法:
•b=tga=对/邻=BC/AC=(Y-a)/X
•bx=Y-a
•Y=a+bx
•当X=1时,BC=b Y=a+b 正好是增加的单位数
 •
•
图解求a、b
(二)最小二乘法求a、b
对于具有线性相关关系的两个变量,可以用回归直线表示它们之间的定量关系,但当将观察值描点于座标图上时,在不知道理论值的情况下,在这些散布点中可以描出无数条近似直线,但事实上只有经过计算求得的理论表达式,才最能代表这些散布点,从理论上讲,这些散布点都是由x、y两个座标决定,这每一个点x所对应的y值与上述所求得的理论直线距离为最小。
•即 ∑(y- )2为最少,因为是2次平方故称为最小二乘法,统计上一般用Q来表示:Q=∑(y- )2=∑(Y-a-bx)2为最小。
为了使Q最小,采用导数求极值办法,先分别对a,b求偏导,然后令其等于零,便可求得联列方程组,进而解出极小值。
1.对a求偏导 dQ/da=2∑(y-a-bx)(-1)=0
2.对b求偏导 dQ/Db=2∑(y-a-bx)(-x)=0
整理得: ∑y=na+b∑x (1)
∑xy=a∑x+b∑x2 (2)
解此联列方程(代入法):
b=[∑xy-1/n∑x∑y]/∑x2-1/n(∑x)2=Lxy/Lxx
代入(1)式得:a=∑y/n-b∑x/n= -b
表5忻州地区76-80年5月份的月均温与粘虫卵量划分等
(一)计算
N=5 =10/5=2 =10/5=2
先求出基本数据:Lxy=∑xy-∑x∑y/n=29-10*10/5=9
Lxx=∑x2-(∑x)2/n=30-102/5=10
Lyy=∑y2-(∑y)2/n=30-102/5=10
根据上表及所求基本数据求解回归斜率b和截距a
b=Lxy/Lxx=9/10=0.9 a=-b=2-0.9*2=0.2
则回归式为: =0.2+0.9x
相关系数为:r=Lxy/Sqr[Lxx.Lyy]=9/Sqr[10*10]=9/10=0.9
查相关系数为:df=3时,r表5%=0.878,r表1%=0.959
结果表明此回归式在5%水平上显著但不达极显著水平。
(三)回归线的精度
知道了x值,不能精确地知道实测值y,但由回归线可以知道y的估计值 ,那么实际的y值高可能有多远呢?也就是用回归预报的精度如何?因为每一个x的实测值的y值按一定的分布在波动(波动规律在一般情况下都认为是正态分布),如果求出波动的标准差,那么回归线的精度就可以估计出来。这种标准差称为“剩余标准差”。
S剩=SQR[1/(n-2)∑(yi- )2]
用上式计算不方便,在实际计算中常用下式
S剩=SQR[(Lyy-bLxy)/(n-2)]=SQR[(1-r2)Lyy/(n-2)]
将上例有关值代入上式求S
S剩=SQR[(10-0.9*9)/(5-2)] =SQR(1.9/3)=SQR(0.633)=0.7956
(四)计算符合率
计算出回归后,还要检验它的符合率。符合率有两种,一种是历史符合率,一种是实际符合率。重要的是后一种,但后一种因为回归式算出后,在实际应用中的次数不会在短时间内达到很多次,因此历史符合率也有很重要的参考价值。两种符合率可用下面公式计算:
表6根据上述资料计算历史符合率
第三节 农业害虫调查中的注意点
一、总体与样本
1、总体:一群性质相同的事物的总和,在统计学上称为“总体”。在害虫调查中常常将一种类型田里发生的某种害虫,当作总体。
2、样本:根据某种害虫在某种作物田里的分布型,按照一定的抽样方法,在调查对象的总体中,抽取一定数量的个体,我们把这个有限个体称做“样本”。
根据样本所查得的结果即能较准确地估计出这 种害虫总体的田间种群密度、发育进度或危害程度。但是,在实际中我们用样本的平均数、方差、变异系数等来表示总体的平均数、方差、变异系数,它们之间的误差称为“抽样误差”。
二、抽样误差的来源
1、抽样方式的不同
取样方式的选择与昆虫在田间的分布型有关,不同的分布型选用不同的抽样方法
2、抽样数目的多少,根据调查要求的精确程度,适当选取一定的样本数目
3、查者的水平、态度,是造成人为误差的来源。
三、常用的抽样方法
1、五点抽样 适合于密集的或成行的植物、害虫分布为随机分布的情况,可按一定的面积、长度或植株数量选取样点
2、对角线抽样 有单对角线和双对角线
3、棋盘式抽样
4、分行抽样(平行线抽样)
5、“Z”字形抽样 适合于害虫分布负二项分布的情况
6、等距抽样
四、常用的抽样单位
1、长度单位 常用生长密集的条播作物
2、面积单位 常用于调查地面或地下害虫
3、体积或容积单位 调查木材或贮粮害虫
4、重量单位 调查粮食和种子中害虫
5、时间单位 活动性大的害虫,观察单位时间内经过、起飞或捕获的虫数
6、以植株、部分植株或植株的某一器官为单位
7、诱集物单位
8、网捕单位
五、抽样方法的分类
1、随机抽样 又称为概率抽样,总体内所有个体均有同等的机会被抽取,即每个抽样单位都具有相等的被抽取的概率
2、顺序抽样 又称机械抽样,按某种既定的顺序抽取一定数量的抽样单位构成样本。分行抽样、等距抽样属此类
3、分层抽样 把研究或调查的总体,按一定的标准分成比较均匀同质的若干部分,即分层,然后,独立地从每一层内随机抽取所确定的抽样数目
六、实验数据的精确度
1、精确度 是指试验中试验数据之间的相近程度。
2、准确度 是指试验数据同总体真值的接近程度,无法估计。
精确度即我们所说的精度,它一般包括两个方面的内容:
其一、要求在试验实施过程中,仔细认真尽量减少外界干扰,使试验结果更符合其田间情况
其二、是在统计分析时,前面数据保留的位数一定等于或大于后边保留的位数。
七、调查和实验数据的统计代换
在实验中得到的数据往往不能符合统计上的基本假定,特别是在方差分析中,其分析必须在线性模型的基础上,即:
1、试验效应和环境效应是可加的,
2、试验的误差应该是随机彼此独立的,而且作正态分布,具有平均数为零
3、所有试验处理必须具有共同的误差方法。即误差同质性
凡不符合以上条件的数据,如果不进行统计处理,往往准确性较差,甚至会得出错误的结论,因此,需要进行统计代换
八、常用的统计代换方法
1、对数代换 适用于负二项分布和奈曼分布及一切非随机性分布的资料
2、百分率代换 就是把每次或每天的调查数据换算成这些数据占总数的百分比
3、百分率的反正弦代换 适用于负二项或潘松分布,其特点是方差与均数不独立,方差随均数的变化而变化
4、平方根代换 适用于潘松分布总体

